今天邀请到雷哥网的GRE数学主讲老师--Helen老师

来给大家讲解下GRE数学中非常重要的一个考点--《等差数列的公式应用》

下面直接安排上干货！！

PART.1 等差数列的公式及其应用

什么是等差数列？大家还记得吗？

等差数列：就是在一组数列里面，每个数和它前面的数字，它的差值都是相等的，每一项和前一项差相等

例如：

a¹   a²   a³...

1       2     3 ...    

这组数列，每个数减掉前一个数都等于1。差值用公差d来表示，也就是每一项减掉它前面这个数字都是相等的，这就是一个等差数列，

注意：等差数列，除了它本身题干上会定义一个等差数列，像我们经常遇到的连续整数或者是连续奇数、连续偶数，甚至是某一个数字的连续的倍数。

比如：三个连续的倍数

 3、6、9...

其实都是等差数列

所以在遇到这些题的时候，那么咱们的这些公式，相应的公式都是可以用上的。

PART.2 习题带练

GRE例题1

答案：A

解题思路：

题干说set T，这个集合T包含的是从11到100 inclusive，就是说临界值都包含进去，11和100都要包含在内的意思。那么就是11到100包含在内。

我们比较的关心的是A和B分别是什么？4倍的T当中4的倍数的数量，以及5倍的T当中5的倍数的数量。就是咱得把4的倍数有多少个，5的倍数有多少个自己能求出来。

怎么去求呢？

其实我们就可以利用等差数列的通项公式去求。

变形之后可以得到关于项数N的一个表达式

n=aⁿ-a¹／d+1

在例1这道题中，就是在t当中，4的倍数，它是连续的11到100，那4的倍数就是

4.8.12.16 ...

其实就是4为公差的一个等差数列，所以这里我们知道哪些信息呢？

在11到100里面，4的最大的倍数就作为这个等差数列的第n项最大的一项。

那我要求项数的话，n等于什么？

aⁿ就是100, a¹ 就是11到100里面4的最小的倍数12,  除以公差4，然后再加1，这样就求出来了

 n=(100-12)/4+1

在这个区间里面，4的倍数具体有多少个，就可以求出来

求出来之后它要求的是4倍，也就在这个基础上再乘以4，算下来之后，就等于92。

Quantity A就算出来了

Quantity B同理可得

我们要算的就是这个区间里面5的倍数，它的个数的五倍，所以是5n

这个区间里面5的倍数最大的是100，最小的是15。

解完之后除以5，然后加1，最后还要乘5

最后等于90

5n=[(100-15)/5+1]*15=90

因此，选A. Quantity A is greater.

因此我们可以得出结论：在一个连续整数区间，某个数字的倍数到底有几个？

是可以用通项公式去求，同样我们说连续的奇数或者是连续的偶数，它同样是一个等差数列。

GRE例题2

答案：A

解题思路：

你可以把它看成是等差数列，再求项数

题干说：J和K都是偶数，并且J＜K，然后问下面是在大于J小于K这个区间里面，偶数的数量是对应哪个选项？

所以我们求的是连续整数的一个区间里面，偶数有几个！

那连续的偶数同样是等差数列，连续偶数公差就等于2了。

然后这道题注意它是greater than j and less than k

也就是说J和K这两个数字本身是不会包含在内

K本来就都是偶数，所以这个区间里面要小于K

最大的偶数就是第n项=K-2

K取不到，只能取比它小的那一个。

最小的是要大于J, 所以J+2

即=（最大的项- 最小的项）/公差

再化简一下，所以对应的是咱们的A选项，就选出来了

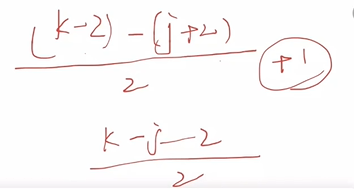
所以同样的在让你求某个区间里面奇数数量或者是偶数数量。

其实可以按照我们等差数列的公式需求，所以这个就是关于等差数列公式的应用

好啦，今天的知识点就分享到这里了！

咨询属于你的GRE课程方案|领取资料 | 解答GRE备考问题 | 加备考群

GRE数学

收藏

分享

报错